|
|
下面我将介绍内嵌物理知识神经网络(PINN)求解微分方程。首先介绍PINN基本方法,并基于Pytorch的PINN求解框架实现求解含时间项的二维方腔流方程。 内嵌物理知识神经网络(PINN)入门及相关论文
- 深度学习求解微分方程系列一:PINN求解框架(Poisson 1d)
- 深度学习求解微分方程系列二:PINN求解burger方程
- 深度学习求解微分方程系列三:PINN求解burger方程逆问题
- 深度学习求解微分方程系列四:基于自适应激活函数PINN求解burger方程逆问题
- 深度学习求解微分方程系列五:PINN求解Navier-Stokes方程正逆问题
- 深度学习求解微分方程系列六:PINN求解波动方程
- 深度学习求解微分方程系列七:PINN求解Beltrami flow方程
- 深度学习求解微分方程系列八:PINN求解Helmholtz方程逆问题
- 深度学习求解微分方程系列九:PINN求解方腔流问题
- 深度学习求解微分方程系列十:PINN求解稳态非稳态圆柱绕流问题
1.PINN简介
神经网络作为一种强大的信息处理工具在计算机视觉、生物医学、 油气工程领域得到广泛应用, 引发多领域技术变革.。深度学习网络具有非常强的学习能力, 不仅能发现物理规律, 还能求解偏微分方程.。近年来,基于深度学习的偏微分方程求解已是研究新热点。内嵌物理知识神经网络(PINN)是一种科学机器在传统数值领域的应用方法,能够用于解决与偏微分方程 (PDE) 相关的各种问题,包括方程求解、参数反演、模型发现、控制与优化等。
2.PINN方法
PINN的主要思想如图1,先构建一个输出结果为 \hat{u} 的神经网络,将其作为PDE解的代理模型,将PDE信息作为约束,编码到神经网络损失函数中进行训练。损失函数主要包括4部分:偏微分结构损失(PDE loss),边值条件损失(BC loss)、初值条件损失(IC loss)以及真实数据条件损失(Data loss)。
特别的,考虑下面这个的PDE问题,其中PDE的解 u(x) 在 \Omega \subset \mathbb{R}^{d} 定义,其中 x=\left(x_{1}, \ldots, x_{d}\right) :
f\left(\mathbf{x} ; \frac{\partial u}{\partial x_{1}}, \ldots, \frac{\partial u}{\partial x_{d}} ; \frac{\partial^{2} u}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} u}{\partial x_{1} \partial x_{d}} \right)=0, \quad \mathbf{x} \in \Omega
同时,满足下面的边界
\mathcal{B}(u, \mathbf{x})=0 \quad \text { on } \quad \partial \Omega
PINN求解过程主要包括:
N_{\Theta}:=L_D \circ \sigma \circ L_{D-1} \circ \sigma \circ \cdots \circ \sigma \circ L_1
式中:
\begin{aligned} L_1(x) &:=W_1 x+b_1, \quad W_1 \in \mathbb{R}^{d_1 \times d}, b_1 \in \mathbb{R}^{d_1} \\ L_i(x) &:=W_i x+b_i, \quad W_i \in \mathbb{R}^{d_i \times d_{i-1}}, b_i \in \mathbb{R}^{d_i}, \forall i=2,3, \cdots D-1, \\ L_D(x) &:=W_D x+b_D, \quad W_D \in \mathbb{R}^{N \times d_{D-1}}, b_D \in \mathbb{R}^N . \end{aligned}
以及 \sigma 为激活函数, W 和 b 为权重和偏差参数。
- 第二步,为了衡量神经网络 \hat{u} 和约束之间的差异,考虑损失函数定义:
\mathcal{L}\left(\boldsymbol{\theta}\right)=w_{f} \mathcal{L}_{PDE}\left(\boldsymbol{\theta}; \mathcal{T}_{f}\right)+w_{i} \mathcal{L}_{IC}\left(\boldsymbol{\theta} ; \mathcal{T}_{i}\right)+w_{b} \mathcal{L}_{BC}\left(\boldsymbol{\theta},; \mathcal{T}_{b}\right)+w_{d} \mathcal{L}_{Data}\left(\boldsymbol{\theta},; \mathcal{T}_{data}\right)
式中:
\begin{aligned} \mathcal{L}_{PDE}\left(\boldsymbol{\theta} ; \mathcal{T}_{f}\right) &=\frac{1}{\left|\mathcal{T}_{f}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{f}}\left\|f\left(\mathbf{x} ; \frac{\partial \hat{u}}{\partial x_{1}}, \ldots, \frac{\partial \hat{u}}{\partial x_{d}} ; \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{d}} \right)\right\|_{2}^{2} \\ \mathcal{L}_{IC}\left(\boldsymbol{\theta}; \mathcal{T}_{i}\right) &=\frac{1}{\left|\mathcal{T}_{i}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{i}}\|\hat{u}(\mathbf{x})-u(\mathbf{x})\|_{2}^{2} \\ \mathcal{L}_{BC}\left(\boldsymbol{\theta}; \mathcal{T}_{b}\right) &=\frac{1}{\left|\mathcal{T}_{b}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{b}}\|\mathcal{B}(\hat{u}, \mathbf{x})\|_{2}^{2}\\ \mathcal{L}_{Data}\left(\boldsymbol{\theta}; \mathcal{T}_{data}\right) &=\frac{1}{\left|\mathcal{T}_{data}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{data}}\|\hat{u}(\mathbf{x})-u(\mathbf{x})\|_{2}^{2} \end{aligned}
w_{f}, w_{i} 、 w_{b} 和 w_{d} 是权重。 \mathcal{T}_{f} , \mathcal{T}_{i} 、 \mathcal{T}_{b} 和 \mathcal{T}_{data} 表示来自PDE,初值、边值以及真值的residual points。这里的 \mathcal{T}_{f} \subset \Omega 是一组预定义的点来衡量神经网络输出 \hat{u} 与PDE的匹配程度。
- 最后,利用梯度优化算法最小化损失函数,直到找到满足预测精度的网络参数 \theta^{*} 。
值得注意的是,对于逆问题,即方程中的某些参数未知。若只知道PDE方程及边界条件,PDE参数未知,该逆问题为非定问题,所以必须要知道其他信息,如部分观测点 u 的值。在这种情况下,PINN做法可将方程中的参数作为未知变量,加到训练器中进行优化,损失函数包括Data loss。
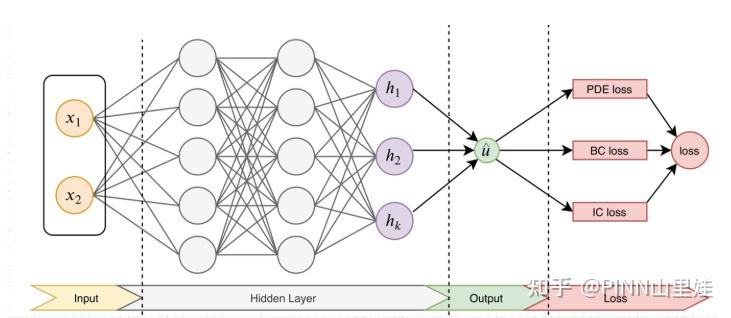
图1:PINN示意图
3.求解问题描述
方腔流体问题可由如下NS方程描述:
u_x + v_y = 0,
u*u_x + v*u_y + p_x/rho - nu*(u_xx + u_yy) = 0,
u*v_x + v*v_y + p_y/rho - nu*(v_xx + v_yy) = 0
其中 (u,v) 为流速,p为压力,x,y范围为[0,1]。对于该问题,Re=100,即rho=1以及nu=0.01.
边界:
- 上边界: u=1,v=0
- 其他边界: u=0,v =0
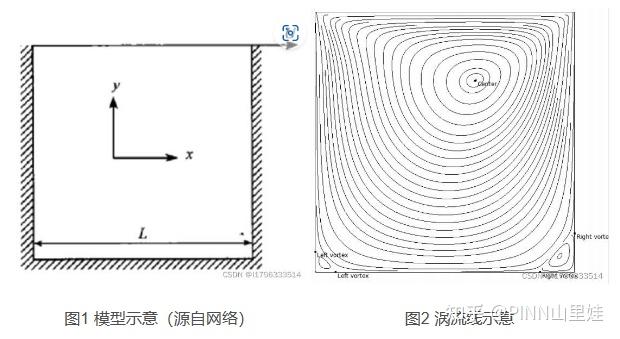
顶盖驱动方腔流是验证流体动力学问题计算方法的一个基准案例。该模型由一个二维方腔组成,其上壁具有切向速度(如图1所示),其他三个壁面速度为零。此运动引起了一种流动现象,其特征是在空腔中心有一个大涡,在角落有一些小涡(如图2所示)。而雷诺数的大小影响着流动中涡的大小和数量。
4.结果展示
实验结果如下图所示,通过训练,PINN能实现u,v,p的准确预测
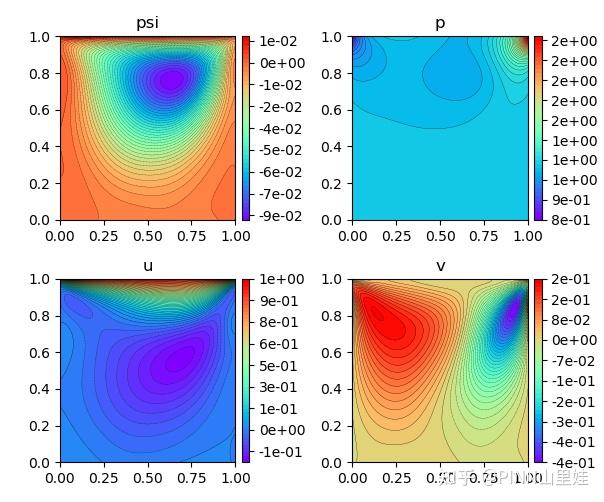 |
|